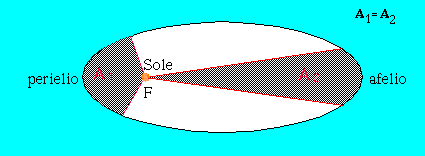

![]() Se consideriamo due pianeti (1 e 2), il rapporto tra le loro accelerazioni
è:
Se consideriamo due pianeti (1 e 2), il rapporto tra le loro accelerazioni
è:
![]() Il secondo principio della dinamica afferma che ad ogni accelerazione
corrisponde una forza ad essa proporzionale; quindi il Sole deve esercitare
sui pianeti una forza proporzionale all'inverso del quadrato della distanza:
Il secondo principio della dinamica afferma che ad ogni accelerazione
corrisponde una forza ad essa proporzionale; quindi il Sole deve esercitare
sui pianeti una forza proporzionale all'inverso del quadrato della distanza:
![]() Newton suppose che la forza dovesse dipendere dalle masse dei corpi ed
enunciò la legge di gravitazione come:
Newton suppose che la forza dovesse dipendere dalle masse dei corpi ed
enunciò la legge di gravitazione come:
Dalla legge di Newton si può ricavare la 3a legge di Keplero:
 Siano m1 la massa di un pianeta e m2
quella del Sole. m1 m2
Siano m1 la massa di un pianeta e m2
quella del Sole. m1 m2
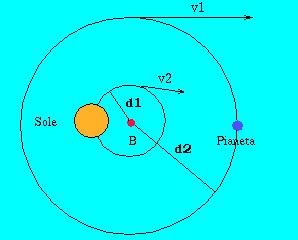
![]() I due corpi formano un sistema che ha il baricentro in B (vedi figura a lato)
e siano d1 e d2 le distanze del
pianeta e del Sole da B; v1 e
v2 siano le
loro velocità di rivoluzione attorno al baricentro.
I due corpi formano un sistema che ha il baricentro in B (vedi figura a lato)
e siano d1 e d2 le distanze del
pianeta e del Sole da B; v1 e
v2 siano le
loro velocità di rivoluzione attorno al baricentro.
![]() Se le orbite sono circolari e P è il periodo di rivoluzione
attorno al baricentro, comune ai due corpi, si ha
Se le orbite sono circolari e P è il periodo di rivoluzione
attorno al baricentro, comune ai due corpi, si ha
d = d1 + d2 =
[G · P2 m2] (m1 + m2)/(4 ·![]() 2
d2)
2
d2)
cioè:
d3 / P2 =
G · (m1 + m2)/4 ·![]() 2
(1)
2
(1)
![]() Che è l'espressione corretta della
3a legge di Keplero. Questa
formula, calcolata con l'assunzione di orbite circolari, è valida
anche in caso di orbite ellittiche.
Che è l'espressione corretta della
3a legge di Keplero. Questa
formula, calcolata con l'assunzione di orbite circolari, è valida
anche in caso di orbite ellittiche.
![]() La massa m2 del Sole è molto più grande della massa di
ognuno dei pianeti, per cui il secondo membro della (1) è costante
per tutti corpi del Sistema Solare. Inoltre, la distanza d coincide
in pratica con la distanza pianeta - Sole.
La massa m2 del Sole è molto più grande della massa di
ognuno dei pianeti, per cui il secondo membro della (1) è costante
per tutti corpi del Sistema Solare. Inoltre, la distanza d coincide
in pratica con la distanza pianeta - Sole.
![]() Dalla (1), noti i valori di d e P e trascurando
m1, la massa m2 del corpo
centrale di un qualsiasi sistema può essere calcolata facilmente.
È possibile, ad esempio, calcolare la massa
del Sole noti i parametri
della Terra o la massa di un pianeta, noti i parametri dei
suoi satelliti.
Dalla (1), noti i valori di d e P e trascurando
m1, la massa m2 del corpo
centrale di un qualsiasi sistema può essere calcolata facilmente.
È possibile, ad esempio, calcolare la massa
del Sole noti i parametri
della Terra o la massa di un pianeta, noti i parametri dei
suoi satelliti.
![]() La determinazione della massa di pianeti sprovvisti di satelliti è
difficile: occorre analizzare le perturbazioni indotte sul pianeta dai
pianeti vicini. L'uso dei satelliti artificiali si è rivelato molto
proficuo per il calcolo della massa: infatti si comportano come satelliti
naturali e i parametri delle loro orbite sono noti con precisione.
La determinazione della massa di pianeti sprovvisti di satelliti è
difficile: occorre analizzare le perturbazioni indotte sul pianeta dai
pianeti vicini. L'uso dei satelliti artificiali si è rivelato molto
proficuo per il calcolo della massa: infatti si comportano come satelliti
naturali e i parametri delle loro orbite sono noti con precisione.